I was looking for a good documentary to watch on Netflix last year. I had seen just about every nature documentary from David Attenborough and I was ready for something a bit more scientific. That’s when I stumbled upon Connected. Every episode was very interesting but there’s one that really blew my mind.
If you analyze a large numerical data set, usually about 30% of those numbers will start with a “1”. Crazy, isn’t it?
This was discovered in 1881 by a Canadian American astronomer named Simon Newcomb who noticed that the first pages of logarithm tables, those starting with a “1”, were more worn than other pages. He also noticed that pages that started with a “2” were more worn than pages that started with any other number than “1” and “2”, and so forth. The tables were used to perform mathematical operations before calculators were invented.
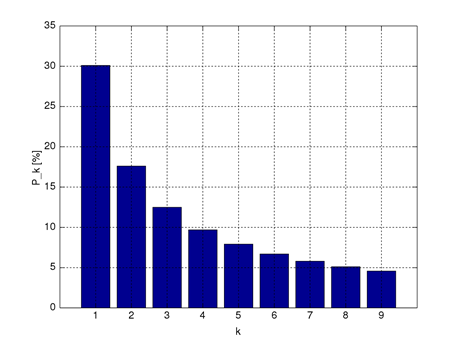
Based on these findings, he established the following pattern, where each bar represents a digit, and the height of the bar is the percentage of numbers that start with that digit:
You would think that there are just as many numbers that start with “1” than numbers that start with a “9”, but this graph shows that you are wrong.
Almost 60 years after Newcomb’s discovery, a physicist named Frank Benford published a paper on this subject and that’s how Benford’s Law was created. I feel bad for Newcomb!
Nowadays, we can put Benford’s Law to good use by uncovering fraud in tax returns and by exposing election fiddling, among other things. Tax returns and election data should follow Benford’s Law and when they don’t, one has to consider the possibility that someone messed with the numbers!
At first, it seemed as though there was no logical reason that could explain this phenomenon but Newcomb and Benford soon made a connection between logarithms and the occurrence of digits. It wasn’t a coincidence that the first pages of the logarithm tables were more worn than the last pages. That’s because people needed to refer to those pages more often than the other pages. But why is that?
It’s important to understand that the values that meet Benford’s Law all evolve in a certain way, with time (such as population increases or decreases), with natural events (such as river erosion), or with economic adjustments (such as a yearly indexations). Their evolution is subject to a multiplier, usually a percentage.
This is where it gets tricky. If you count the number of multiplications that are needed to get from 10 to 20, using a multiplier of 1.01 (a 1% increase), you will very quickly realize that you need a lot more than that to get from 90 to 100. If you start with 10 and you keep on multiplying the cumulative value by 1.01, you need to repeat this about 70 times before you finally get to 20 (10, 10.1, 10.201, 10.30301, 10.4060401, 10.5101005, etc.). With a starting value of 50, you will only need to perform this multiplication about 18 times before you get to 60, and with 90, you will reach 100 in less than 11 multiplications.
This demonstrates that for all things that evolve using a multiplier, there are many more steps required to make the first digit of a number go from 1 to 2, than from 2 to 3, and so forth. If you add up all the multiplications needed to go from 10 to 20, from 20 to 30, all the way to the last ten numbers from 90 to 100, you get to a total of 235 multiplications. You see where this is going: 30% of the multiplications were required for the first tranche of numbers (10-20), 17.5% for the second one (20-30), and 4.6% for the last one (90-100).
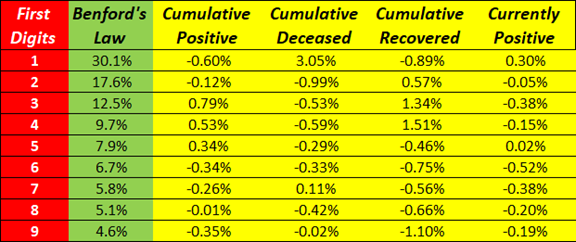
I was so baffled by this that I wanted to test it myself. I downloaded a gigantic data set containing over 350,000 lines of COVID data. I then created formulas in Excel to compile the frequency of digits and lo and behold, the data set complied with Benford’s Law.
See for yourself. The percentages of Benford’s Law exact occurrences are in green, and the actual differences between Benford’s Law percentages and the percentages of occurrence of COVID cases are in orange.
If you don’t believe me or you’re just curious to see if it’ll work with another data set, you can go to https://data.europa.eu/data/datasets and search for a large numerical data set for which you would expect all the values to start with a “1” through a “9” exactly 11.1% of the time. You could use electricity bills, death rates, lengths of rivers, but you couldn’t use telephone numbers or annual salaries.
If you’re unable to achieve Benford’s Law percentages after multiple attempts, it’s either because you’re using the wrong data set, your formulas are incorrect, or you’ve just unknowingly proven another theory: Murphy’s Law!